Sebelumnya... dari kalian semua ada yang tahu tentang fluida gak ? Kalau tahu yaudah.... selesai. Maaf, cuma bercanda :). Fluida itu adalah segala sesuatu yang dapat MENGALIR dan memberikan HAMBATAN terhadap perubahan bentuk benda ketika mengalami TEKANAN. Jadi air, sirup, kecap, bahkan udara pun merupakan contoh fluida. Fluida itu sendiri dibedakan menjadi dua, yakni fluida statis dan fluida dinamis. Kali ini, saya hanya akan membahas fluida statis alias benda "mengalir" yang dalam kondisi "tidak mengalir"
Untuk kawan-kawan semua, adakah yang ingat rumus ini?
 Yap... rumus diatas adalah rumus untuk mencari tekanan. Dengan pemberian gaya F yang tetap, semakin kecil luas permukaan benda A maka semakin besar tekanan P yang dialami benda tersebut. Maka dari itu, gaya berbanding lurus dengan tekanan tetapi tekanan berbanding terbalik dengan luas permukaan benda. Contoh dari penerapan tekanan ini adalah pembuatan paku atau pasak. Mengapa ujungnya runcing? Jelas agar paku atau pasak tersebut masuk. Tapi bagaimana cara kerjanya? Kembali lagi penjelasan di atas. Agar menimbulkan tekanan maksimal, maka gaya yang terjadi harus sebesar-besarnya dan luas permukaannya harus sesempit-sempitnya (
Yap... rumus diatas adalah rumus untuk mencari tekanan. Dengan pemberian gaya F yang tetap, semakin kecil luas permukaan benda A maka semakin besar tekanan P yang dialami benda tersebut. Maka dari itu, gaya berbanding lurus dengan tekanan tetapi tekanan berbanding terbalik dengan luas permukaan benda. Contoh dari penerapan tekanan ini adalah pembuatan paku atau pasak. Mengapa ujungnya runcing? Jelas agar paku atau pasak tersebut masuk. Tapi bagaimana cara kerjanya? Kembali lagi penjelasan di atas. Agar menimbulkan tekanan maksimal, maka gaya yang terjadi harus sebesar-besarnya dan luas permukaannya harus sesempit-sempitnya (ohh... pantas saja ujungnya runcing).
Apa hubungannya dengan fluida? Seperti yang sudah saya jelaskan, bahwa fluida itu memberikan HAMBATAN terhadap perubahan bentuk benda ketika mengalami TEKANAN kan... Misalkan paku(yah.. paku lagi) tersebut kita celupkan ke dalam suatu wadah air. Gaya yang timbul pada benda yang tercelup akan mengarah ke segala arah termasuk juga ke atas karena tekanan di dalam fluida.
Atmosfer adalah contoh nyata dalam penerapan fluida. Atmosferr memiliki 5 lapisan yang mana urutannya (dari yang dekat dengan permukaan bumi) adalah troposfer, stratosfer, termosfer, ionosfer, dan eksosfer. Dan lapisan atmosfer yang bertekanan tinggi adalah troposfer. Hal ini dikarenakan lapisan troposfer "menopang" lapisan-lapisan yang lainnnya.
Pada contoh lainnya, adalah air pada wadah silinder. Anggap air itu berlapis-lapis (ingat-ingat). Lapisan terbawah mengalami tekanan yang besar karena harus "menopang" lapisan diatasnya. Sedangkan lapisan paling atas mengalami tekanan yang terkecil, yang ada hanya ada tekanan atmosfer (tekanan yang diberikan atmosfer). Suatu benda yang ada di bumi pasti terpengaruh oleh gaya gravitasi bumi. Semakin rendah ketinggian suatu benda di bumi, maka gaya gravitasinya semakin besar. Tak terkecuali fluida. Pada lapisan yang terbawah, akan mengalami gaya gravitasi yang besar pula. Hal tersebut dapat dikatakan sebagai tekanan hidrostatika.
| Apa yang kalian pikirkan tentang gambar diatas? |
Apa hubungannya dengan fluida? Seperti yang sudah saya jelaskan, bahwa fluida itu memberikan HAMBATAN terhadap perubahan bentuk benda ketika mengalami TEKANAN kan... Misalkan paku
Atmosfer adalah contoh nyata dalam penerapan fluida. Atmosferr memiliki 5 lapisan yang mana urutannya (dari yang dekat dengan permukaan bumi) adalah troposfer, stratosfer, termosfer, ionosfer, dan eksosfer. Dan lapisan atmosfer yang bertekanan tinggi adalah troposfer. Hal ini dikarenakan lapisan troposfer "menopang" lapisan-lapisan yang lainnnya.
Pada contoh lainnya, adalah air pada wadah silinder. Anggap air itu berlapis-lapis (ingat-ingat). Lapisan terbawah mengalami tekanan yang besar karena harus "menopang" lapisan diatasnya. Sedangkan lapisan paling atas mengalami tekanan yang terkecil, yang ada hanya ada tekanan atmosfer (tekanan yang diberikan atmosfer). Suatu benda yang ada di bumi pasti terpengaruh oleh gaya gravitasi bumi. Semakin rendah ketinggian suatu benda di bumi, maka gaya gravitasinya semakin besar. Tak terkecuali fluida. Pada lapisan yang terbawah, akan mengalami gaya gravitasi yang besar pula. Hal tersebut dapat dikatakan sebagai tekanan hidrostatika.
 |
| Anggap ae banyu nang wadah iku berlapis-lapis ;) (editan jelek... I don't care) |
Nah ... sekarang yuk hitung besar hitung besar tekanan di sembarang titik (misal titik A). Air yang mempunyai massa jenis  . Misalnya kita akan menghitung tekanan hidrostatika di titik A yang berada di ketinggian h dari permukaan fluida. Misalkan, kita dapat membuat silinder datar (ingat bahwa fluida dianggap sebagai lapisan) yang berluas A sedemikian rupa sehingga berimpitan dengan titik A. Tekanan hidrostatika yang bekerja pada silinder datar dihasilkan oleh berat silinder itu sendiri. Berat silinder dapat dihitung dengan cara dibawah :
. Misalnya kita akan menghitung tekanan hidrostatika di titik A yang berada di ketinggian h dari permukaan fluida. Misalkan, kita dapat membuat silinder datar (ingat bahwa fluida dianggap sebagai lapisan) yang berluas A sedemikian rupa sehingga berimpitan dengan titik A. Tekanan hidrostatika yang bekerja pada silinder datar dihasilkan oleh berat silinder itu sendiri. Berat silinder dapat dihitung dengan cara dibawah :

dengan :
 = tekanan hidrostatika (
= tekanan hidrostatika ( = Pa) (1 atm = 76 cmHg = 1,013 x
= Pa) (1 atm = 76 cmHg = 1,013 x  Pa = 1,013 bar)
Pa = 1,013 bar)
g = percepatan gravitasi ( )
)
A = luas penampang ( )
)
Perhatikan keempat bejana di bawah ! Meski bentuknya berbeda-beda, tetapi tekanan di ketinggian masing-masing wadah adalah sama. Pada gambar, tekanan di titik A, B, C, maupun D adalah sama meski berbeda wadah. Jadi semua titik yang terletak pada suatu bidang datar di dalam zat cair yang sejenis memiliki tekanan yang sama. Dalam hal ini yang mempengaruhi bukannya bentuk bejana melainkan ketinggian.
Tekanan pada persamaan (1) adalah tekanan hidrostatika yangmana tekanan atmosfernya belum dihitung. Lah... trus tekanan yang sebenarnya gimana ? Caranya adalah menjumlahkan tekanan atmosfer saat itu dengan tekanan hidrostatika. Tada.... ketemu nich yang namanya tekanan total alias tekanan absolut.

dengan P adalah tekanan absolut dan adalah tekanan atmosfer saat itu.
adalah tekanan atmosfer saat itu.
Persamaan hidrostatis di atas dapat diturunkan melalui gambar di bawah ini :
Menurut persamaan hidrostatika tekanan di titik A dan di titik B bergantung pada massa jenis zat dan ketinggian fluida di dalam tabung (percepatan gravitasi dapat diabaikan karena ketinggian dari dasar fluida adalah sama). Maka secara matematis dapat ditulis sebagai berikut :




Dengan :
 = massa jenis zat fluida A
= massa jenis zat fluida A
 = massa jenis zat fluida B
= massa jenis zat fluida B
 = jarak titik A dengan permukaan fluida
= jarak titik A dengan permukaan fluida
 = jarak titik B dengan permukaan fluida
= jarak titik B dengan permukaan fluida
Sementara penerapannya adalah sebagai manometer pipa terbuka, barometer, dan pengukur tekanan ban.
http://ws-budi.blogspot.com/2012/01/tekanan-hidrostatik.html
http://perpustakaancyber.blogspot.com/2013/03/pengertian-fluida-statis-dan-dinamis-massa-jenis-tekanan-hidrostatis-total-aplikasi-tegangan-permukaan-contoh-soal-kunci-jawaban.html
Saripudin, Aip, dkk. 2009. Praktis Belajar Fisika 2 SMA/MA. Jakarta : Pusat Perbukuan Departemen Pendidikan Nasional
Supiyanto. 2007. Fisika SMA Jilid 2. Jakarta: Phibeta
Widodo, Tri. 2009. Fisika untuk SMA/MA Kelas XI. Jakarta : Pusat Perbukuan Departemen Pendidikan Nasional
dan berbagai sumber referensi yang "terpecaya"
Berat silinder 
Dari persamaan di atas, besar tekanan hidrostatika di titik A sama dengan :
dengan :
g = percepatan gravitasi (
A = luas penampang (
h = kedalaman fluida dari permukaan atas fluida (m)
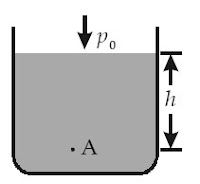 |
| Tekanan hidrostatik di titik A |
 |
| Bejana satu berbentuk silinder, bejana dua sisi-sisinya ada yang menggelembung, bejana tiga agak miring, kalau yang keempat..... deskripsikan sendirilah :) |
dengan P adalah tekanan absolut dan
Persamaan hidrostatis di atas dapat diturunkan melalui gambar di bawah ini :
 |
| Gambar sing nang nduwur iku nunjukno bahwa tekanan nang titik A iku podho karo nang titik B |
Dengan :
Sementara penerapannya adalah sebagai manometer pipa terbuka, barometer, dan pengukur tekanan ban.
- Manometer pipa terbuka
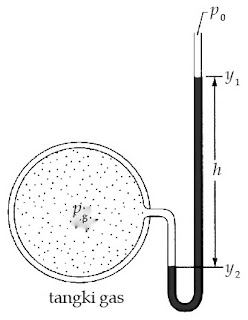
Alat ini digunakan sebagai alat untuk mengukur tekanan udara .Ujung yang satu mendapat tekanan sebesar p (dari gas yang hendak diukur tekanannya) dan ujung lainnya berhubungan dengan tekanan atmosfir (p0).Besarnya tekanan udara di titik y1 = p0, sedangkan tekanan udara di titik y2 = p. y1 memiliki selisih ketinggian Δy1 = 0 dan y2 memiliki selisih ketinggian Δy2 = h. Berdasarkan persamaan tekanan hidrostatik, besarnya tekanan udara dalam tabung pada gambar di atas dinyatakan dengan persamaan berikut ini.dengan ρ adalah massa jenis zat cair di dalam tabung.
- Barometer

Barometer raksa ini ditemukan pada 1643 oleh Evangelista Torricelli, seorang ahli Fisika dan Matematika dari Italia. Ia mendefinisikan tekanan atmosfir dalam bukunya yang berjudul "A Unit of Measurement, The Torr" Tekanan atmosfer (1 atm) sama dengan tekanan hidrostatis raksa (mercury) yang tingginya 760 mm. Cara mengonversikan satuannya adalah sebagai berikut :ρ raksa × percepatan gravitasi Bumi × panjang raksa dalam tabungatau(13.600 kg/cm3 )(9,8 m/s2)(0,76 m) = 1,103 × 105 N/m2Jadi, 1 atm = 76 cmHg = 1,013 × 105 N/m2
- Pengukur tekanan ban
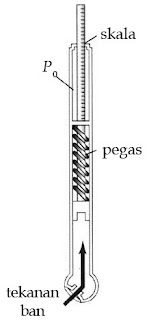
Alat ini digunakan untuk mengukur tekanan udara di dalam ban. Bentuknya berupa silinder panjang yang di dalamnya terdapat pegas. Saat ujungnya ditekankan pada pentil ban, tekanan udara dari dalam ban akan masuk ke dalam silinder dan menekan pegas. Besarnya tekanan yang diterima oleh pegas akan diteruskan ke ujung lain dari silinder yang dihubungkan dengan skala. Skala ini telah dikalibrasi sehingga dapat menunjukkan nilai selisih tekanan udara luar (atmosfer) dengan tekanan udara dalam ban.
Okay, selanjutnya saya akan membahas mengenai Hukum Pascal. Penemu Hukum Pascal ini (yang tak lain dan tak bukan) adalah Om Pascal lah... Om yang punya nama panjang Blaise Pascal ini melakukan percobaan fluida tabung U. Lalu berdasarkan percobaannya, Om Pascal berkesimpulan bahwa apabila tekanan diberikan pada fluida yang memenuhi sebuah ruangan tertutup, tekanan tersebut akan diteruskan oleh fluida tersebut ke segala arah dengan besar yang sama tanpa mengalami pengurangan. Perhatikan gambar kalau pingin lebih jelasnya.
Secara matematis dapat ditulis persamaan :

Dengan :
Berbagai alat diciptakan berdasarkan Hukum Pascal ini yaitu :
 |
| Pipa sing digawe Pakde Pascal gawe percobaanne |
Dengan :
F1 = gaya yang dikerjakan pada pipa 1
F2 = gaya yang dikerjakan pada pipa 2
A1 = luas penampang pada pipa 1
A2 = luas penampang pada pipa 2Berbagai alat diciptakan berdasarkan Hukum Pascal ini yaitu :
- Dongkrak Hidrolik

Dongkrak hidrolik merupakan salah satu aplikasi sederhana dari Hukum Pascal. Berikut ini prinsip kerja dongkrak hidrolik. Saat pengisap kecil diberi gaya tekan, gaya tersebut akan diteruskan oleh fluida (minyak) yang terdapat di dalam pompa. Akibatnya, minyak dalam dongkrak akan menghasilkan gaya angkat pada pengisap besar dan dapat mengangkat beban di atasnya. - Mesin Hidrolik Penangkat Mobil

Mesin hidrolik pengangkat mobil ini memiliki prinsip yang sama dengan dongkrak hidrolik. Perbedaannya terletak pada perbandingan luas penampang pengisap yang digunakan. Pada mesin pengangkat mobil, perbandingan antara luas penampang kedua pengisap sangat besar sehingga gaya angkat yang dihasilkan pada pipa berpenampang besar dan dapat digunakan untuk mengangkat mobil. - Rem Hidrolik
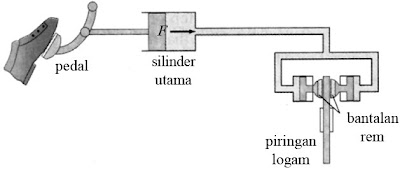
Rem hidrolik digunakan pada mobil. Ketika Anda menekan pedal rem, gaya yang Anda berikan pada pedal akan diteruskan ke silinder utama yang berisi minyak rem. Selanjutnya, minyak rem tersebut akan menekan bantalan rem yang dihubungkan pada sebuah piringan logam sehingga timbul gesekan antara bantalan rem dengan piringan logam. Gaya gesek ini akhirnya akan menghentikan putaran roda.
Yapch... Sekian dulu dari saya. Oh iya, saya lampirkan juga video yang berkaitan dengan materi kali ini... ^_^
PERCOBAAN TEKANAN HIDROSTATIKA
PEMBAHASAN TEKANAN HIDROSTATIKA
HUKUM PASCAL
HUKUM PASCAL DAN REM HIDROLIK
HUKUM PASCAL DAN REM HIDROLIK
So, if you have any opinions or questions please leave the comment.
Source :http://ws-budi.blogspot.com/2012/01/tekanan-hidrostatik.html
http://perpustakaancyber.blogspot.com/2013/03/pengertian-fluida-statis-dan-dinamis-massa-jenis-tekanan-hidrostatis-total-aplikasi-tegangan-permukaan-contoh-soal-kunci-jawaban.html
Saripudin, Aip, dkk. 2009. Praktis Belajar Fisika 2 SMA/MA. Jakarta : Pusat Perbukuan Departemen Pendidikan Nasional
Supiyanto. 2007. Fisika SMA Jilid 2. Jakarta: Phibeta
Widodo, Tri. 2009. Fisika untuk SMA/MA Kelas XI. Jakarta : Pusat Perbukuan Departemen Pendidikan Nasional
dan berbagai sumber referensi yang "terpecaya"
No comments:
Post a Comment